As a bunch of engineers we love running tests. It brightens our day to finally find out if our ideas for better performance actually delivers the goods. A lot of the time we have to go back to the drawing board (or, nowadays, Solidworks),but some of the time things turn out pretty good. In fact, this winter we began construction a new test chamber. We’ve successfully exceeded the limits of our current chamber, and need to be able to accurately gauge much higher and much lower airflow (relative to our whole house fans) for some new designs and products we have in development.
Our sales team often fields calls from interested homeowners wondering why our fans are so much larger than our competitors’, which often promise equal or better performance. So we want to take a moment to offer our explanation for the this difference. Considering the time and energy we commit to R&D, it can be a little frustrating for us to be constantly explaining why, but our explanation is simple: Our fans are bigger because they have to be, physically, to deliver the performance we certify they do, and we’re skeptical, extremely skeptical, of other manufacturers’ performance claims.
Here’s why:
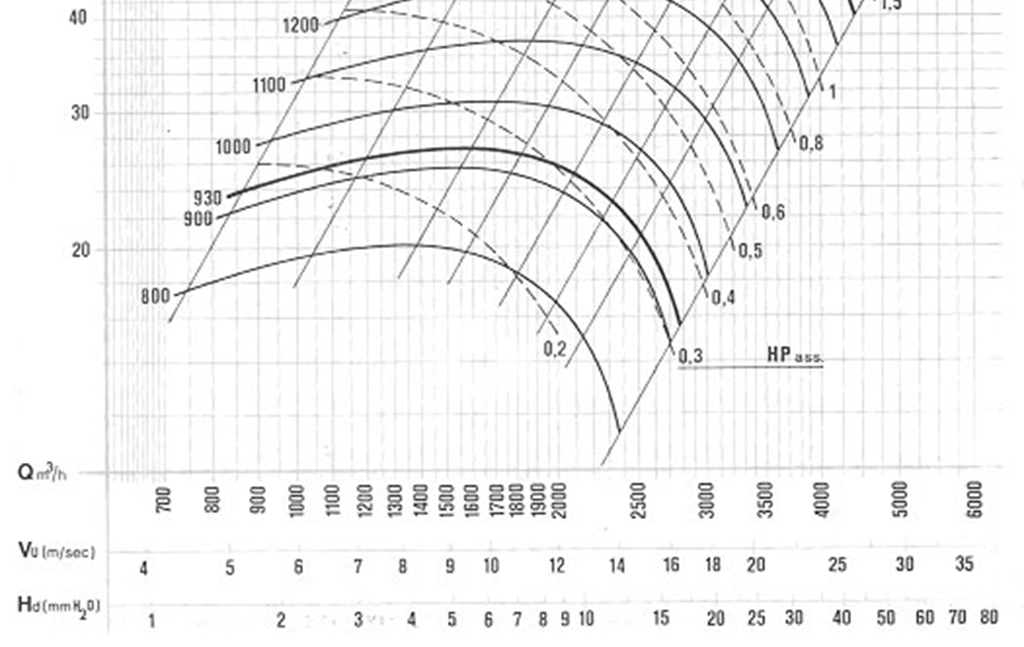
The performance of all fans is governed by a set of physics equations known as the “Affinity Laws”. These equations set out the relationship between a fan’s diameter, how fast it spins, how much airflow it produces, and at what power. There are three of these laws and they are: With a little bit of algebra we can move the elements in these equations around to transform them into new equations, just as enlightening. The derivative equation we’re most interested in for our purposes here is below (we’ll let the p1/p2 term fall out of our equation from this point forward, as all of our performance specs are published as adjusted to a standard air density).
With a little bit of algebra we can move the elements in these equations around to transform them into new equations, just as enlightening. The derivative equation we’re most interested in for our purposes here is below (we’ll let the p1/p2 term fall out of our equation from this point forward, as all of our performance specs are published as adjusted to a standard air density).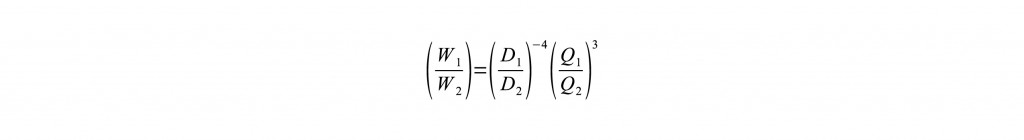 Now, we said above that we’re very skeptical of some of other manufacturers’ performance claims. The equation above is why. Consider, for example, our 5.0e fan. This fan is our most power and most efficient. At its highest speed, the 5.0e moves 5064.9 cubic feet of air per minute. Its motor draws 809.8 watts to accomplish this, giving it an efficiency of 6.25 cfm/watt. One of another manufacturer’s fan’s published specifications claim it moves 4816 cfm while drawing 477 watts (10.10 cfm/watt), which is fine as far as things go, except for the fact it uses only an 18.5″ diameter fan blade, while our 5.0e’s blade is 24″ diameter.
Now, we said above that we’re very skeptical of some of other manufacturers’ performance claims. The equation above is why. Consider, for example, our 5.0e fan. This fan is our most power and most efficient. At its highest speed, the 5.0e moves 5064.9 cubic feet of air per minute. Its motor draws 809.8 watts to accomplish this, giving it an efficiency of 6.25 cfm/watt. One of another manufacturer’s fan’s published specifications claim it moves 4816 cfm while drawing 477 watts (10.10 cfm/watt), which is fine as far as things go, except for the fact it uses only an 18.5″ diameter fan blade, while our 5.0e’s blade is 24″ diameter.
When see such differences in performance, our first instinct is to ask ourselves how we might be able to improve our own performance. For our 5.0e to achieve 10.10 cfm/watt efficiency on high, it would have to move the same 5064.9 cfm while drawing only 501.48 watts. This is a lot less than 809.8! We could improve our fan’s performance by changing the diameter of its fan blade, but what would the diameter need to be? Let’s do the math.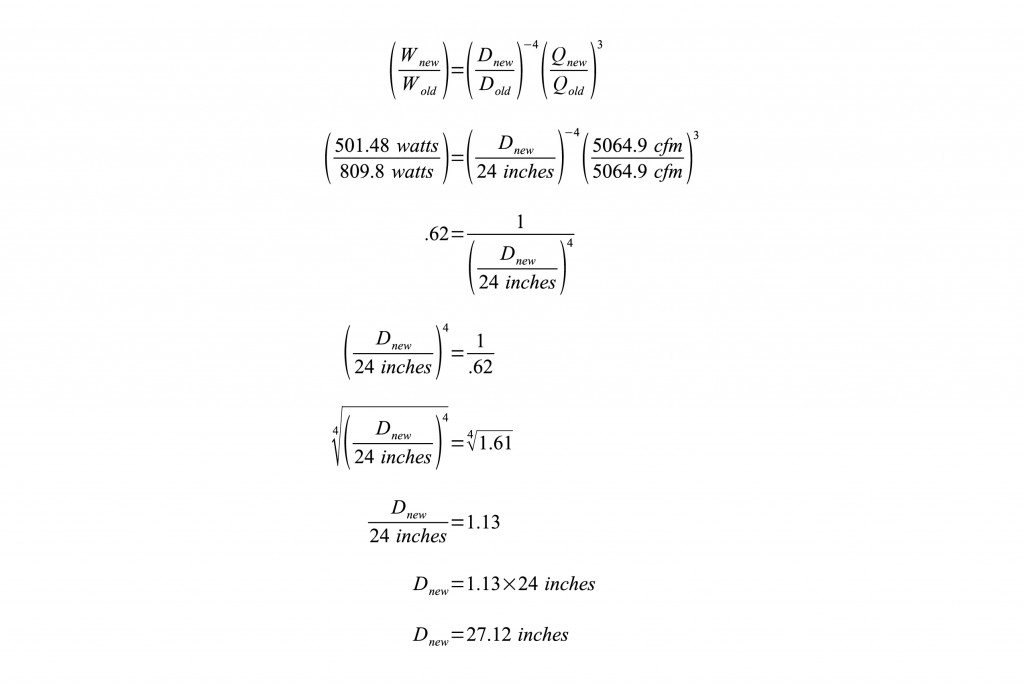 The mathematics above show that, in order for our 5.0e fan to move 5064.9 cfm at the other fan’s 10.10 cfm/watt efficiency, the diameter of its blade would have to be 27.12 inches. That’s three inches larger than it is now! In fact, to simply just match the other fan’s 4816 cfm at 477 watts, the 5.0e’s blade would have to be 26.4 inches in diameter (our math is here). The diagram below visually depicts the difference between these for diameters.
The mathematics above show that, in order for our 5.0e fan to move 5064.9 cfm at the other fan’s 10.10 cfm/watt efficiency, the diameter of its blade would have to be 27.12 inches. That’s three inches larger than it is now! In fact, to simply just match the other fan’s 4816 cfm at 477 watts, the 5.0e’s blade would have to be 26.4 inches in diameter (our math is here). The diagram below visually depicts the difference between these for diameters.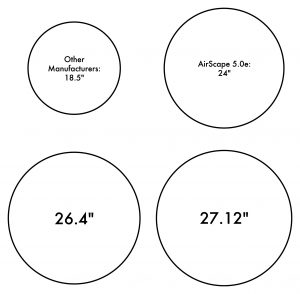 How does a fan that is only 18.5″ in diameter achieve performance that would seem to require a 26.4″ diameter fan? Well, that’s why we are “extremely” skeptical of these performance claims. The fan affinity laws are laws of physics, they cannot be broken. Science is science to everybody.
How does a fan that is only 18.5″ in diameter achieve performance that would seem to require a 26.4″ diameter fan? Well, that’s why we are “extremely” skeptical of these performance claims. The fan affinity laws are laws of physics, they cannot be broken. Science is science to everybody.
So what would be the consequences if the other manufacturer’s performance claims were incorrect? Quite a lot actually. If we were to reduce our 5.0e’s fan diameter to 18.5 inches, it would require 1992.11 watts to move 4816 cfm. That’s over four times as much electricity the other manufacturer claims its fan uses to move the same amount of air. Translated into dollars and cents, this is the difference between a fan that costs 7.32¢ per hour to operate, and a fan which costs 30.56¢ to operate (at a cost of electricity of 15.34¢/kwh).
That’s a lot of money, considering a whole house fan is intended to be run for hours at a time on most (if not all) evenings during a large portion of the year. The graph below visually shows just how big this difference is.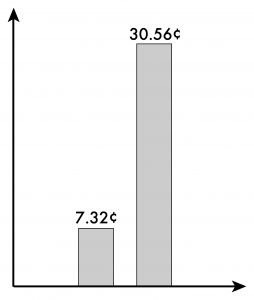 Likewise, if we were to reduce 5.0e’s diameter to 18.5 inches, 477 watts of power would only move 2988.29 cfm. That’s nearly 38% less than claimed! To meet the requirements of the State of California’s Energy Code (aka “Title 24”), a new house must have a whole house fan capable of exhausting 2 cfm per sq. foot of conditioned floor area in the home. The difference here is the difference between a fan that can be used to meet the code requirements for a house up to 2408 sq. ft., and a fan that can only be used to meet these requirements in a home up to 1494 sq. feet. If you installed this fan in your 2400 sq. ft. home—thinking it was capable of the greater airflow—not only would your home not be code-compliant, but your fan would be very ineffective. Such a low amount of airflow relative to the size of the home would do little to cool it.
Likewise, if we were to reduce 5.0e’s diameter to 18.5 inches, 477 watts of power would only move 2988.29 cfm. That’s nearly 38% less than claimed! To meet the requirements of the State of California’s Energy Code (aka “Title 24”), a new house must have a whole house fan capable of exhausting 2 cfm per sq. foot of conditioned floor area in the home. The difference here is the difference between a fan that can be used to meet the code requirements for a house up to 2408 sq. ft., and a fan that can only be used to meet these requirements in a home up to 1494 sq. feet. If you installed this fan in your 2400 sq. ft. home—thinking it was capable of the greater airflow—not only would your home not be code-compliant, but your fan would be very ineffective. Such a low amount of airflow relative to the size of the home would do little to cool it.

You can double-check our math for the above here and here. If you’d like, you can even come check out our new test chamber; our address is 625 Charles Way, Medford, Oregon. Until then, please enjoy a picture of it under construction.
At any rate, we hope this blog has helps you to understand why our fans are so much larger than other manufacturers’: they simply have to be to produce the airflows they do. And this is the same reason why we are so skeptical of those other manufacturers’ performance claims: they simply don’t seem to add up. We’d encourage you to be similarly skeptical, and to consider one of our fans for cooling your home this summer. If you find the mathematics above even a tiny bit confusing, please contact us. We’d be happy to walk through the numbers with you, and we’d love the opportunity to discuss the many other advantages AirScape whole house fans offer over other available brands.